April 30, 2023
The Python Heap Data Structure: A Comprehensive Guide
In computer science, a heap is a specialized tree-like data structure that satisfies the heap property. It is used as a priority queue to efficiently find the maximum or minimum value of a set of values. A heap can be implemented as an array where each element represents a node in the tree, and the children of each node can be found at positions 2i+1 and 2i+2. The heap property ensures that the value of each node is greater or smaller than its children depending on whether it is a max heap or min heap, respectively.
Types of Heap
There are two types of Heap: Max Heap and Min Heap. In a Max Heap, the parent node is always greater than or equal to its child nodes, while in a Min Heap, the parent node is always less than or equal to its child nodes. Both types of Heap have their own unique characteristics and can be used in a variety of algorithms.

Generating a Heap
In Python, the heapq module from the standard library provides an implementation of the heap queue algorithm, also known as the priority queue algorithm [0]. The heapq module can turn a regular list into a heap, where the smallest element is at index 0. Here’s an example of creating a heap in Python using the heapify() function:
import heapq
li = [5, 7, 9, 1, 3]
heapq.heapify(li)
print(li)
You can also create an empty list and use the heappush() function to add elements to the heap. The heappop() function removes and returns the smallest element from the heap while maintaining the heap invariant [source]. Here’s an example:
import heapq
new_heap = []
heapq.heappush(new_heap, 2)
heapq.heappush(new_heap, 3)
heapq.heappush(new_heap, 7)
heapq.heappush(new_heap, 9)
print(heapq.heappop(new_heap)) # Output: 2
print(heapq.heappop(new_heap)) # Output: 3
The heappushpop() function can be used to push an element onto the heap and then immediately pop and return the smallest element [0]. The heapreplace() function can be used to pop and return the smallest element and then push a new element onto the heap [0].
In Python, heaps can be classified as either min-heaps or max-heaps. In a min-heap, the smallest element is at the root, while in a max-heap, the largest element is at the root [1]. The heapq module in Python implements a min-heap by default, where the smallest element is at index 0. To create a max-heap, you can negate the values of the elements in the list to be transformed into a heap [1].
Heap Operations
There are several operations that can be performed on a Heap, including insertion, deletion, heapify, and extract max/min.
Insertion
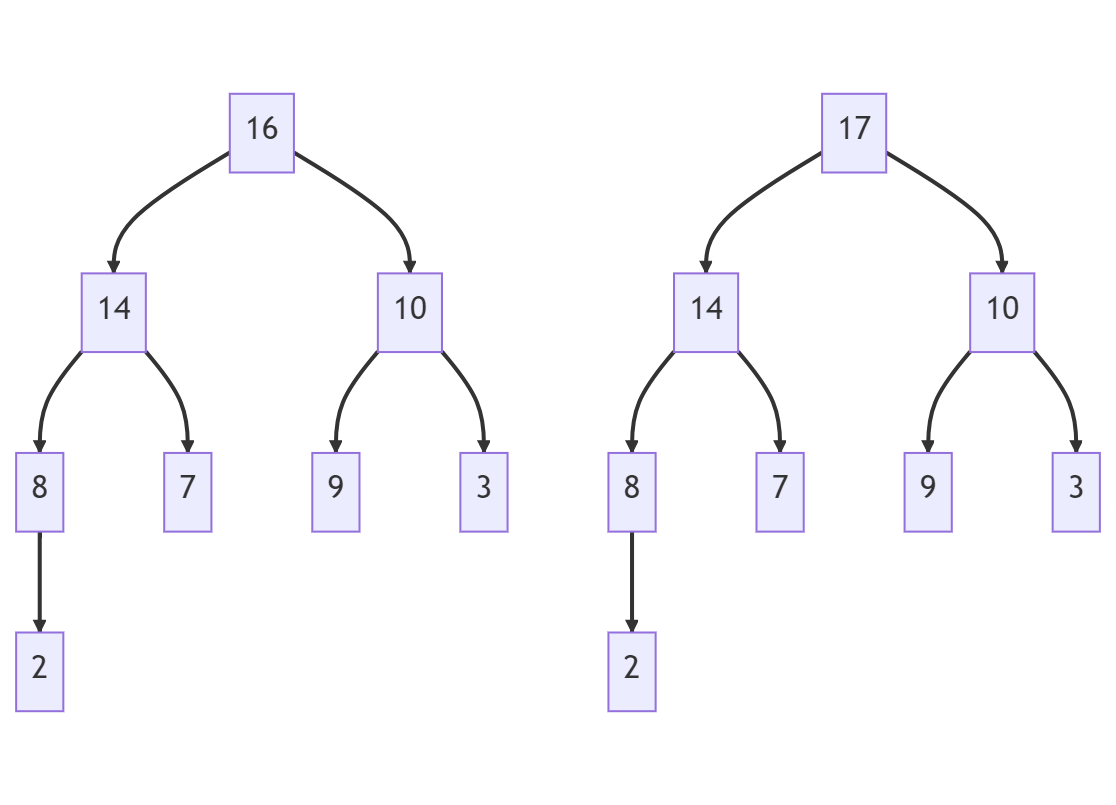
To insert an element into a Heap, we first add it to the bottom level of the Heap in the leftmost open spot. We then compare the new element with its parent node, and if the Heap property is violated, we swap the two nodes. We repeat this process until the Heap property is satisfied.
To make an insertion in a priority queue implemented with a heap, you need to add the item as a new node of the tree and place it just beyond the rightmost node at the bottom level of the tree or as the leftmost position of a new level if the bottom level is already full. After this action, the tree is complete, but it may violate the heap-order property. Hence, unless the position is the root of the tree, you need to compare the key at position p to that of p’s parent. If the key at p is greater than or equal to the key at q, the heap-order property is satisfied, and the algorithm terminates. If instead, the key at p is less than the key at q, then you need to restore the heap-order property, which can be locally achieved by swapping the entries stored at positions p and q.

Deletion
To delete an element from a Heap, we first replace the element with the last element in the Heap. We then compare the new element with its parent node, and if the Heap property is violated, we swap the two nodes. We repeat this process until the Heap property is satisfied.
To remove a node from a heap, you need to ensure that the shape of the heap respects the complete binary tree property by deleting the leaf at the last position of the tree. Then, to preserve the item from the last position, you copy it to the root in place of the item with the minimum key that is being removed by the operation. After this step, you may need to perform down-heap bubbling to restore the heap-order property. You can achieve this by swapping the entries stored at the root and its child with the minimal key.
Heapify
Heapify is the process of creating a Heap from an unsorted array. We start by building a complete binary tree from the array. We then iterate over the non-leaf nodes in reverse order and perform the sift-down operation until the Heap property is satisfied.
Extract Max/Min
Extract Max/Min is the process of removing the root node from the Heap. For a Max Heap, this is the maximum element in the Heap, while for a Min Heap, this is the minimum element in the Heap. After removing the root node, we replace it with the last element in the Heap and perform the sift-down operation until the Heap property is satisfied.
Heap Implementation
There are several ways to implement a Heap, including array-based implementation, binary Heap implementation, and Fibonacci Heap implementation.
Array-based implementation
In an array-based implementation, we represent the Heap as an array, where the root node is at index 0, and the left and right child nodes of a parent node at index i are at indices 2i+1 and 2i+2, respectively.
Binary Heap implementation
In a binary Heap implementation, we represent the Heap as a binary tree, where the root node is at the top of the tree, and each node has at most two child nodes.
Fibonacci Heap implementation
In a Fibonacci Heap implementation, we represent the Heap as a collection of trees, where each tree satisfies the Min Heap property.
Heapq Module
Like we used in the example above. The Heapq module is a built-in Python module that provides functions for working with heaps. It can be used to implement priority queues, which are data structures that allow you to quickly access the elements with the highest or lowest priority.
Applications of Heap
The Heap data structure is widely used in computer science algorithms, including sorting algorithms, priority queues, and graph algorithms.
Sorting algorithms
HeapSort is a sorting algorithm that uses the Heap data structure. It works by first creating a Max Heap from the unsorted array, then repeatedly extracting the maximum element and placing it at the end of the sorted array.
Priority Queues
A priority queue is a data structure that allows us to insert and extract elements with a priority value. The Heap data structure is commonly used to implement a priority queue, where the highest priority element is always at the root node of the Heap.
Graph algorithms
The Heap data structure is also used in various graph algorithms, including Dijkstra’s algorithm for finding the shortest path in a graph, Prim’s algorithm for finding the minimum spanning tree of a graph, and Kruskal’s algorithm for finding the minimum spanning tree of a graph using a disjoint-set data structure.
Pros and Cons of Heap
Like any data structure, the Heap has its advantages and disadvantages.
Advantages
- The Heap data structure has a relatively small memory footprint compared to other data structures.
- The Heap data structure provides efficient insertion, deletion, and extraction of elements with O(log n) time complexity.
- The Heap data structure can be easily implemented using an array, making it a simple and efficient data structure.
Disadvantages
- The Heap data structure has poor cache locality, which can result in slow performance when accessing elements in memory.
- The Heap data structure does not support efficient searching of elements. To search for an element, we must perform a linear search over the entire Heap, resulting in O(n) time complexity.
Conclusion
The Heap data structure is a specialized tree-based data structure that is commonly used in computer science algorithms. It provides efficient insertion, deletion, and extraction of elements and can be used in a variety of applications, including sorting algorithms, priority queues, and graph algorithms. Despite its advantages, the Heap data structure also has its limitations, including poor cache locality and lack of support for efficient searching.
Understanding the Heap data structure is essential for any computer science student or professional, and its applications can be seen in various algorithms and applications.