How Markov Decision Processes Power Reinforcement Learning

---

How Does an AI Learn to Make Smart Choices?

Have you ever taught a pet a new trick? Imagine you’re training your dog to roll over. You give the command, and the dog, a bit confused at first, might just sit or lie down. You offer no treat. Then, it shuffles and accidentally rolls onto its side. You give it a treat and some praise. After a few more tries, it connects the action of rolling over with the delicious reward. Through this simple process of trial, error, and feedback, the dog learns the desired behavior.

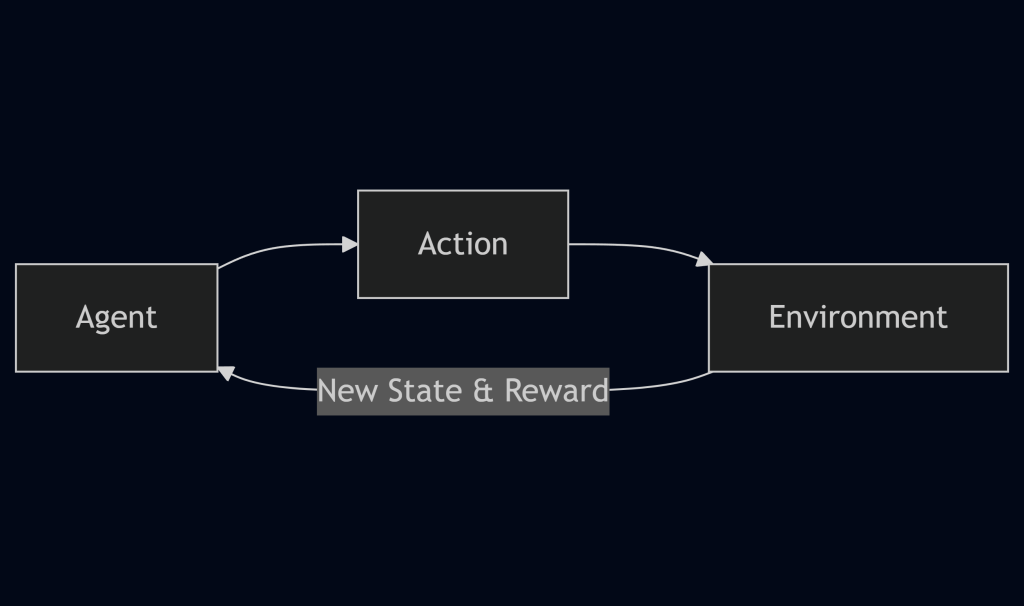
At its core, this is exactly how a major branch of artificial intelligence called Reinforcement Learning (RL) works. It’s a powerful technique that teaches an AI, or an agent, to make smart decisions by interacting with its world, or environment.³ The agent is the learner like the dog in our example and the environment is everything it interacts with, such as the living room it’s in.⁵ The learning process unfolds in a continuous loop: the agent takes an action, the environment responds with a new situation and a reward (or penalty), and the agent uses this feedback to update its strategy.⁶

But this raises a critical question: how can a computer, which thrives on logic and precise instructions, navigate a world that is often messy, random, and unpredictable? An AI can’t just “get a feel for it” like a dog can. It needs a structured set of rules, a kind of map for its environment. This is where the Markov Decision Process (MDP) comes in. An MDP is the mathematical framework that acts as the “map and rulebook” for the agent’s world.⁸ It doesn’t solve the problem itself, but it describes the problem in a language the AI can understand, providing the essential structure for learning to begin.¹⁰

The true power of the MDP lies in its elegant approach to simplifying reality. The real world is infinitely complex; to make a perfect decision, an agent might theoretically need to remember every single thing that has ever happened to it.¹³ Imagine trying to find your car in a massive parking lot. Your current location isn’t enough; you need to remember where you parked it hours ago.¹³ Modeling this endless stream of history is computationally impossible.¹⁴ The MDP framework makes a brilliant trade-off by introducing a powerful assumption: the

Markov Property.⁸ This property states that we can define a “state” that summarizes all the important information from the past. By focusing only on the current state, we can discard the full history, dramatically simplifying the problem and making it solvable.⁹ Therefore, creating an MDP is an act of useful abstraction, where the designer’s main challenge is to capture the essence of a problem without getting lost in the noise.¹⁶

Meet Our Agent: A Robot Vacuum on a Mission

To make these abstract ideas concrete, let’s follow the journey of a single, consistent agent: a robotic vacuum cleaner tasked with cleaning a small room.¹⁰ This analogy is a classic in AI because it’s visual, intuitive, and perfectly encapsulates the challenges of decision-making under uncertainty.¹¹

Let’s lay out the “game board” for our robot. The environment is a simple 4×3 grid. This room has a few key features:

• Empty, clean tiles the robot can move on.
• Dirty tiles that need to be cleaned.
• Obstacles, like walls or furniture, that the robot cannot pass through.¹²
• A special goal square: the charging station, where the robot can recharge its battery.¹²
• A designated starting position.¹¹

The robot’s mission is clear: clean all the dirty tiles and finish at its charging station, all while using the fewest moves possible and avoiding collisions with walls.¹¹

This seemingly simple scenario is a perfect microcosm of real-world decision problems because it contains all the necessary complexities of an MDP. First, it involves uncertainty. We can imagine the robot has “slippery wheels,” meaning its motors aren’t perfect. When it tries to move forward, it might succeed, or it might accidentally veer left or right.¹¹ Because of this randomness, the robot can’t just follow a pre-programmed set of instructions; it needs a flexible strategy that can adapt when things go wrong.

Second, it involves conflicting goals. The robot gets a positive reward for cleaning a tile and a large bonus for reaching its charger, but it gets a negative penalty for bumping into a wall.¹² The fastest path to the last dirty spot might be dangerously close to an obstacle, forcing the robot to weigh the potential reward against the risk of a penalty. This need to make trade offs between immediate gains, long-term objectives, and potential dangers is the very essence of intelligent decision making that MDPs are designed to model.

The Five Building Blocks of the Robot’s World (and any MDP)

Every Markov Decision Process, whether it’s for a simple robot or a complex financial trading system, is defined by five key components. Let’s break them down using our vacuum cleaner example.

States (S): “Where am I right now?”

A state is a complete description of the agent’s situation at a specific moment a snapshot of the world from the agent’s perspective.⁴ For our robot, a state is simply its location, or (x, y) coordinate, on the grid.¹¹ The starting point could be state (1,1), a dirty tile could be at (3,2), and the charging station could be at (4,3).

The golden rule governing states is the Markov Property. This crucial assumption says that the current state provides all the information needed to make an optimal decision about the future.⁸ In other words, the past doesn’t matter, as long as you know where you are right now. A great analogy is a game of chess.¹⁵ To decide your next move, you only need to look at the current positions of the pieces on the board. You don’t need to know the exact sequence of moves that led to this configuration. The current board is a complete “state.” For our robot, its current location is all it needs to decide its next action.²¹

Actions (A): “What can I do from here?”

Actions are the set of choices the agent can make from a given state.⁸ In any grid cell, our robot has a set of available actions:

Move UP, Move DOWN, Move LEFT, or Move RIGHT.¹¹ The set of available actions can change depending on the state. For instance, if the robot is next to a wall, the action

Move UP might result in it bumping the wall and staying in the same place.¹²

Transition Probabilities (P): “What are my chances?”

This component is what makes the world interesting and unpredictable. The transition probability, often written as P(s′∣s,a), defines the chance of moving to a new state, s′, after taking action a in the current state s.⁹ Because of the “slippery floor” we mentioned, the robot’s actions are not guaranteed to succeed.

Let’s define the probabilities for our robot. When it tries to Move UP:

• There is an 80% probability it moves UP successfully.
• There is a 10% probability its wheels slip, causing it to move LEFT instead.
• There is a 10% probability its wheels slip, causing it to move RIGHT instead.¹¹

This element of chance is precisely why the agent needs more than just a fixed script. It requires a dynamic strategy a policy that can navigate an environment where the outcomes of its actions are uncertain.²⁵

Rewards (R): “Was that a good move?”

A reward is a numerical signal the agent receives from the environment after taking an action.³ This feedback tells the agent whether its move was good (a positive reward) or bad (a negative reward, or penalty).¹¹ The agent’s entire goal is to accumulate the highest possible total reward over time.

For our robot, we can define a clear reward structure:

• Reaching the charging station: +50 (a big prize for completing the main goal).
• Cleaning a dirty tile: +10 (a solid reward for making progress).
• Bumping into a wall: -5 (a penalty to discourage bad moves).
• Making any other move (e.g., moving to an already clean tile): -1 (a small “cost of living” penalty to encourage efficiency and discourage wasting time).¹¹

This reward function is the only way a human designer can communicate the desired goal to the agent. The agent doesn’t understand “cleaning” or “efficiency”; it only understands its single-minded objective: maximize the final score.³ Crafting this function is a delicate art. For example, in a chess-playing AI, if you reward the agent for taking the opponent’s pieces, it might learn to sacrifice its king just to capture a pawn a behavior that maximizes the immediate reward but fails the ultimate goal of winning the game.³ The small

-1 penalty for each move our robot makes is a form of “reward shaping.” It nudges the robot to find the shortest path, preventing it from wandering aimlessly on clean tiles just because there is no penalty for doing so.

The Discount Factor (γ): “Is a reward now better than a reward later?”

The discount factor is a number between 0 and 1 that represents the agent’s “patience”.²² A simple analogy is that $10 today is more valuable to most people than the promise of $10 a year from now. The discount factor applies the same logic to the agent’s rewards, making immediate feedback more valuable than rewards it might receive far in the future.³ This not only encourages the agent to achieve goals more quickly but also serves a crucial mathematical purpose: it prevents the total reward from spiraling to infinity in tasks that could potentially go on forever.³

To bring it all together, here is a simple table summarizing the five building blocks of our robot’s MDP:

Component	Description	Example in the Robot’s World
State	A unique situation the agent can be in.	The robot’s current coordinate, e.g., (3, 4).
Action	A choice the agent can make from a state.	Move UP, DOWN, LEFT, or RIGHT.
Reward	The feedback for a transition.	+50 for reaching the charger, -5 for hitting a wall.
Transition Probability	The likelihood of an action leading to a new state.	When moving UP: 80% chance of success, 10% slip left, 10% slip right.
Policy	The agent’s strategy mapping states to actions.	A complete plan, like a map with an arrow in every square showing the best move.

The Agent’s Brain: Crafting a Winning Strategy (Policy)

Now that we have described the robot’s world using the five components of an MDP, the final piece of the puzzle is the policy. A policy, denoted by the Greek letter π, is the agent’s brain—its complete strategy for how to behave.²⁹ It is a rule that tells the agent what action to take in every possible state it might find itself in.³¹ You can visualize it as a finished map of the robot’s grid world, with an arrow drawn in every single square, pointing in the direction the robot should go.

Policies can be straightforward or complex. A deterministic policy is the simplest kind: for any given state, the action is fixed. For example, “In state (2,2), always go RIGHT“.⁹ A

stochastic policy, on the other hand, chooses actions based on probabilities, such as, “In state (2,2), go RIGHT 70% of the time and UP 30% of the time.” This randomness can be very useful for helping an agent explore its environment and discover new, better strategies.⁹

The entire purpose of reinforcement learning is to find the optimal policy, denoted as π∗. This is the one strategy that will earn the agent the highest possible cumulative reward over the long run.²⁷ For our robot, an optimal policy would be a complete set of instructions that expertly navigates the slippery floor, cleans every dirty tile, avoids all walls, and reaches the charger in the most efficient way possible, perfectly balancing all the risks and rewards we defined. The agent finds this policy by learning the “value” of being in each state and the value of taking each action from each state. The optimal policy is then simply to always choose the action that leads to the best expected future reward.²

This final, optimal policy is more than just a set of rules; it is the compressed, distilled wisdom the agent has gained through all its trial-and-error interactions. When the agent starts, its policy is random and useless it knows nothing.³³ To learn, it must first

explore by trying actions it’s unsure about to gather information.¹⁰ As it receives rewards, it begins to learn which actions are good, and it must then

exploit this knowledge to maximize its score.¹⁰ This creates the famous

exploration-exploitation dilemma.⁷ If an agent only exploits what it already knows, it might get stuck in a suboptimal routine like a quiz show contestant who quits after winning $100, never discovering the $1 million prize at the end.⁶ If it only explores, it never cashes in on its discoveries. The learning process is an algorithmic approach to balancing this trade-off, and the optimal policy is the final product the embodiment of all the intelligence it has learned.

Why MDPs are a Game Changer for AI

The Markov Decision Process is the essential first step that transforms a messy, real-world challenge into a structured problem that an AI can tackle.⁶ It provides the fundamental language—states, actions, rewards, and probabilities that powerful reinforcement learning algorithms are built to understand.⁹ Algorithms like

Q-Learning, Value Iteration, and Policy Iteration are the engines designed to “solve” the MDP by taking the map and its rules and methodically finding the optimal policy, π∗.⁹ The MDP frames the puzzle, and the RL algorithm solves it.

The power of this framework extends far beyond robotic vacuums. Countless complex problems can be modeled as MDPs, making it a cornerstone of modern AI. Here are just a few examples:

• Robotics: An industrial robot arm learns the optimal sequence of movements to assemble a product, where states are joint positions and actions are motor commands.¹⁵
• Finance: An automated trading system decides whether to buy, sell, or hold assets based on current market conditions (the state) to maximize profit.³⁹
• Inventory Management: A warehouse system learns the best time to reorder stock to meet fluctuating demand without overspending.⁶
• Healthcare: AI systems can help devise personalized treatment plans, where a patient’s health metrics are the state and different therapies are the actions.¹¹
• Autonomous Driving: A self-driving car decides whether to accelerate, brake, or change lanes based on the state of traffic, pedestrians, and road signs.³
• Gaming: AI agents learn to master incredibly complex games like Go and chess by treating the board configuration as the state and legal moves as actions.¹⁵

Ultimately, the Markov Decision Process is the foundational bedrock of modern reinforcement learning. By providing a simple yet profoundly effective way to frame the puzzle of making decisions under uncertainty, it gives our AI agents the “rules of the game” they need to learn, adapt, and make truly intelligent choices.