Given the root of a binary tree, return the inorder traversal of its nodes’ values.

The inorder traversal of a binary tree is the nodes in the tree listed in the order they would be visited by an inorder traversal. To solve this problem, we can use a stack to keep track of the nodes we have visited. We will push the root node onto the stack and then pop it off when we are done visiting its left subtree. We will then visit the right subtree of the root.
In this blog post, we will solve leetcode question 94 – Binary Tree Inorder Traversal. This is a classic computer science problem that can be solved using a number of different algorithms. We will discuss two different solutions – a recursive solution and an iterative solution. Let’s get started!
Simplifying the problem
Leetcode 94 question asks us to traverse a binary tree in order. In order to make this easier, let’s simplify the problem by thinking about it as traversing a linked list instead of a binary tree. We can think of each node in the tree as having two pointers – one pointing to the left child and one pointing to the right child.
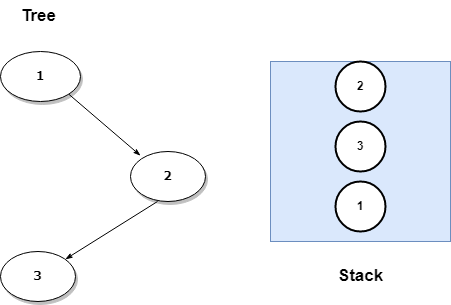
We are placingall the left nodes of the current node into stack. node is now null since we keep assigning node to its left node after placing the current node into stack.
Solutions
Recursive Solution
The recursive solution for leetcode 94 is a straightforward one. We can use a simple recursive function to traverse the binary tree in order from left to right. We start by visiting the left-most node and then recursively call our function on each of its children (the left and right nodes). This will cause our function to traverse the tree in order from left to right.
Iterative Solution
The iterative solution for leetcode 94 is slightly more complex, but still manageable. We can use a stack to store our current node and its children (the left and right nodes). We start by pushing the root node of the binary tree onto the stack and then while the stack is not empty, we pop a node off of it. We then process it by printing its value and pushing its left and right nodes (if they are not null) onto the stack. Then, when there are no more nodes on the stack, our inorder traversal will be complete.
Solution one is using a stack. Here is the code in JavaScript
var inorderTraversal = function(root) {
var stack = [];
var result = [];
// while there is a root or there are still nodes in the stack
while(root || stack.length){
// while there is a root
// push the root into the stack
// and set the root to the root's left child
while(root){
stack.push(root);
root = root.left;
}
// set the root to the node at the top of the stack
root = stack.pop();
// push the root's value into the result array
result.push(root.val);
// set the root to the root's right child
root = root.right;
}
return result;
};
Code in Python
def inorderTraversal(self, root):
"""
:type root: TreeNode
:rtype: List[int]
"""
result, stack = [], [(root, False)]
while stack:
root, is_visited = stack.pop()
if root is None:
continue
if is_visited:
result.append(root.val)
else:
stack.append((root.right, False))
stack.append((root, True))
stack.append((root.left, False))
return result
Code in Java
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
while(root != null || !stack.isEmpty()){
while(root != null){
stack.push(root);
root = root.left;
}
root = stack.pop();
result.add(root.val);
root = root.right;
}
return result;
}
The time complexity is O(n) and the space complexity is O(n).